Wavelengths In Our Rooms

We have updated this blog since its original posting to reflect new information gathered in regards to the length of sound waves. This blog was updated on 11/19/19.

Sound Energy

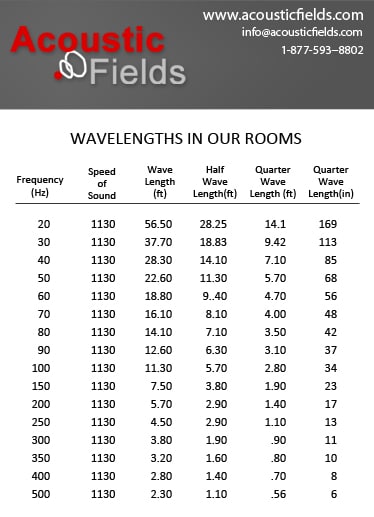
Sound energy is divided into frequencies. Each frequency has a given size or length. The speed of sound, 1130 ft./sec., stays constant and is used to calculate the length of a particular frequency. To find the length of a given frequency, we take the speed of sound, 1130 ft./sec. and divide it by the specific frequency we want to find the length of. If we use 20 Hz. as our frequency, we take the speed of sound 1130 ft./sec. and divide it by 20. Our answer is 56.5 ft. This means that 20 Hz. wave has a wavelength of 56.5′. How does this 20 Hz or 56.5′ wave fit into our home theater, listening, or professional recording studio? The answer is that it does not and never will.

Wave Theory

There is a theory that will help us understand how sound waves react inside our rooms. It is termed wave theory or wavelength theory. It is divided into the full-wave, half wave, and quarter wavelength sections to attempt to explain all the side effects that different sized waves produce in enclosed spaces such as our home theater, listening rooms, or professional recording studios. If we examine our 20 Hz. wave with its 56.5′ length then logically we need to have a room that has a 57′ length in order to let this low-frequency wave run to its total length uninhibited by any room boundary surface. Unfortunately, most of our rooms that we record or playback music in do not have a 56.5′ dimension anywhere. This is an example of a full-wave theory.

Sound Energy: https://en.wikipedia.org/wiki/Sound_energy

Low-Frequency Waves

After our 20 Hz. wave leaves our speakers or any sound generating device and is produced into our room with its 30′ length, we know that for the first 30′ the wave will run for 30′ until it hits a room boundary surface or wall. At this point, the wave is then bounced back into the room and has to travel another 30′ back to the source. With its first 30′ full run deducted from the 56.5′ total wavelength, we have 26.5′ left to continue back into the room. With a 30′ length back in room distance, we have 26.5′ left in the wavelength distance to go freely with leaving 3.5′ remaining. Half wavelength theory would say that in order to have a flat room response down to 20 cycles, we need to have a room that has a room dimension of at least 30′ in order to not have any side effects by cramming the long length of sound waves into a small room, because at least half of the wave will have the distance to run free twice, once up and once back. Quarter wavelength applies the same rational using 25% of the respective wave’s length.

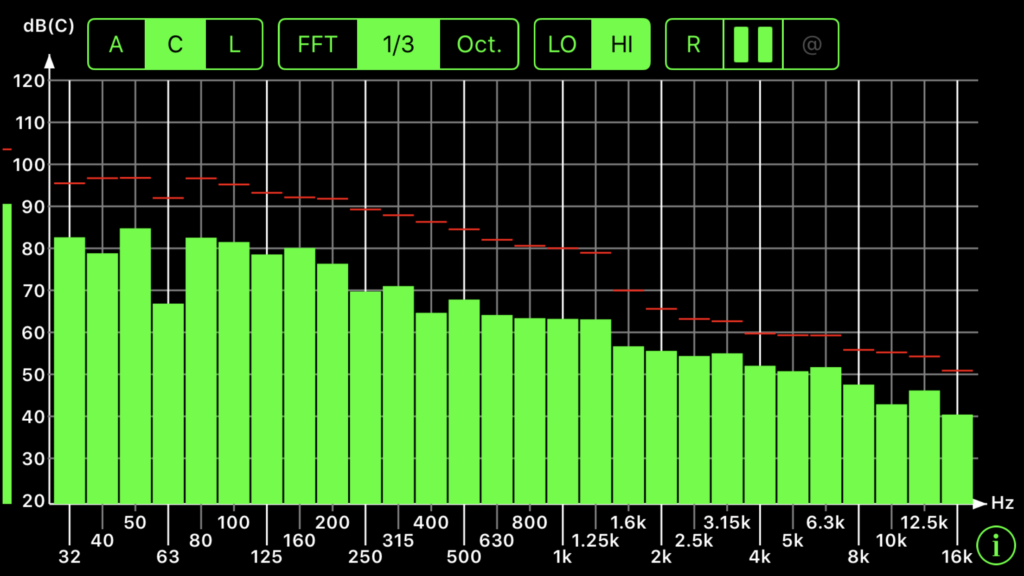
Octave Bands

Room Modes

If we do not have at least half wavelength distances within our rooms to accommodate especially low-frequency waves, we will have the waves telling us that they are not happy with the accommodations we have given them. They will do this by producing resonances that tell us they think their quarters are too cramped. They will produce resonances between each of our room boundary surfaces. If the resonances they produce occur between two parallel surfaces, they are termed axial resonances. Resonances produced between four surfaces are termed tangential resonances and resonances from six surfaces are termed oblique. The issues these resonances produce are called room modes and modes are produced by what is termed standing waves. Standing waves are produced because the length of sound waves does not fit within the room dimensions.

Waves and Rays; https://acousticfields.com/waves-and-rays/

Pressure Build Up

If wavelengths do not have at least half of their wavelengths to run back and forth they can bump into themselves. This continual bumping into themselves causes the wavelengths to stand around if you will and not keep moving through the room. When wavelengths stand around, the sound pressure created by this process causes unwanted effects. Room modes can have two major effects on the sound in our home theater, listening rooms, or professional recording environments. These modes are determined by the length of sound waves or acoustic wavelengths.

Too Much Energy

First, room modes can exaggerate certain frequency ranges. These exaggerations or gain if you will overwhelm surrounding frequencies and smother them to the point where they can not be heard at all. If one places a microphone within one of these modes, certain frequencies will not be heard at all and some frequencies will be too prominent in the recording. Bass boom is an example of a room modal issue that can smother and can exaggerate certain frequencies.

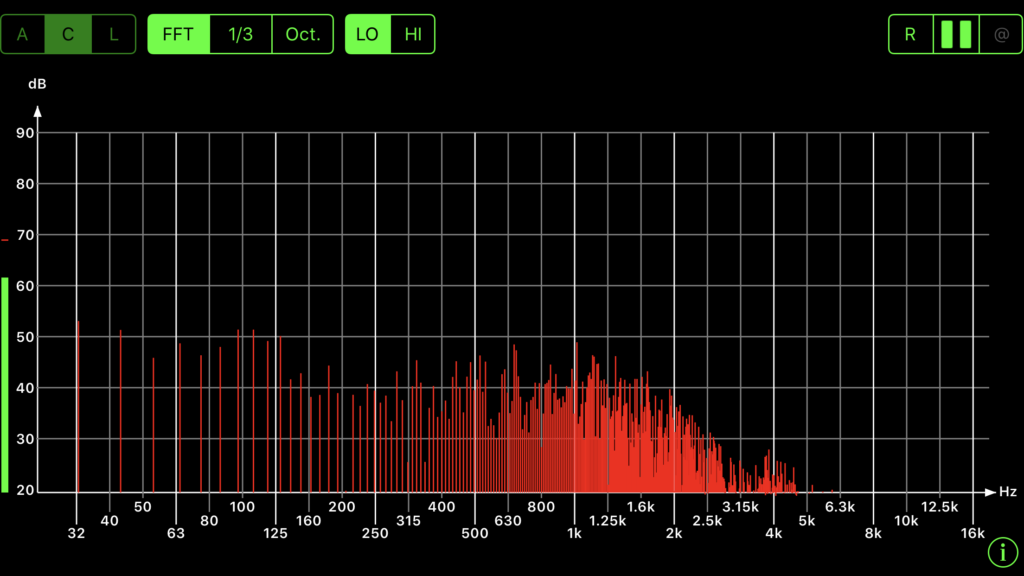
Frequencies

Where Did It Go

Room modes can also smother higher frequencies above the room modal frequency. A 30 cycle wave can blur and smear a 50 Hz. wavelength and not allow any information from this wavelength to be heard at all. These lower frequency resonances are common in rooms and that is the reason that bass sounds bad in most rooms. Continue low-pressure build-up affects the attack and decay of each individual low-frequency note. Low-frequency sound energy can be heard but one must allow for each notes appropriate attack and decay rates to be realized by reducing the sound pressure created by the build-up of the room contained energy.

Wavelengths in our room need distance to travel freely and not be influenced by our room boundary surfaces such as our walls, ceilings, and floors. In an ideal acoustical world, with full acoustic wavelength theory applied, all frequencies have the full wavelength distance to travel. We could have this scenario if we had rooms that had 60′ distances in height, width, and length and we wanted a room completely flat down to 20 Hz. Unfortunately, real estate is expensive and reality is much different. The half-wave theory allows for half the wavelength distance to travel freely and then bounce back towards the source and then fall short of the next boundary. Half-wave theory must be the minimum governing consideration when we are seeking a flat room response at certain frequencies especially those below 100 cycles in our home theater, listening, or recording studios.

In Summary

I hope today’s discussion helped. Please message me at info@acousticfields.com if you have any questions as I am always happy to help. If you want more to learn more about room acoustics please sign up for our free acoustic video training series and ebook. Upon sign up you will instantly have access to a series of videos and training to help improve the sound in your studio, listening room or home theatre.